2021全国100所名校最新高考模拟示范卷三理综

2021全国100所名校最新高考模拟示范卷三理综，目前我们已经整理了2021全国100所名校最新高考模拟示范卷三理综的各科答案和试卷，更多100所最新高考模拟示范请关注本网站。

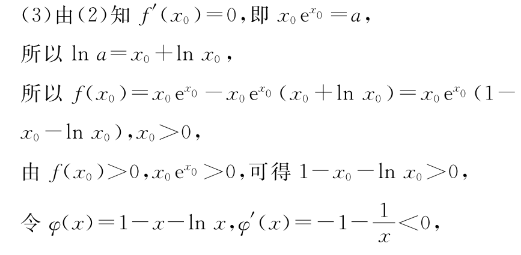
22.解:(1)当a=0时f(x)=xe,则f(x)=(x 1)e,所以f(1)=e,f(1)=2e,所以函数f(x)在x=1处的切线方程为y-e=2e(x1),即2ex-y-e=0.(3分)(2)f(x)=(x 1)ex-a(1 )=(x 1)(e-)=(x 1)(xe-a),x>0,x①当a≤0时f(x)>0,f(x)在区间(0, ∞)上单调递增,不存在极值②当a>0,令f(x)=0,则xe=a,令g(x)=xe-a,g(x)=(x 1)e2>0,g(x)单调递增,又因为g(0)=-a<0,g(a)=a(e-1)>0,必存在x>0,使g(x)=0,x∈(0,x0),g(x)<0,(x)<0,f(x)单调递减,x∈(x, ∞),g(x)>0,f(x)>0,f(x)单调递增,所以x=x是f(x)的极小值点,综上所述:当a≤0时,f(x)无极值点;当a>0时,f(x)有一个极值点(7分)(3)由(2)知f(x)=0,即xoe0=a,所以lna=xo lnxo,所以f(xo)= xo o-xoo(x lnx)=xoe0(1 xo-In xo), xo >0,由f(x)>0,xoe>0,可得1-xo-lnx>0,令q(x)=1-x-lnx,(x)=-1-<0,显然q(x)在区间(0, ∞)上单调递减,而(1)=0,由(x)>(1),所以0 1时,H(x)>0,函数H(x)单调递增,0 x 1>0,因为x∈(0,1),所以e>x0 1>0,1-x0-lnx>1-x0 1-x>0,两式相乘可得eo(1-x-lnx0)>(x0 1)(22x),所以f(x)=xoea(1-xo-lnx0)>2x0(x0 1)(1x0)=2(x0-x),即f(x)>2(x0-x)(12分)