2022届金学导航·压轴卷(二)·D区专用理科数学答案

2022届金学导航·压轴卷(二)·D区专用理科数学答案，目前答案易对网已经整理了2022届金学导航·压轴卷(二)·D区专用理科数学答案的各科答案和试卷，更多联考试卷请关注本网站。

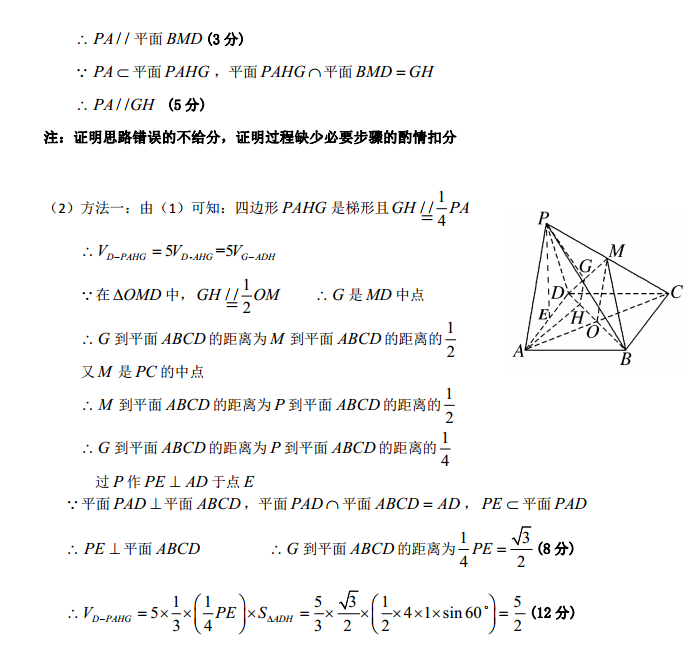
9.解析(1)证明:如图所示,连接AC交BD于点O,连接OM四边形ABCD是平行四边DO是AC的中点又M是PC的中点∴.PAOM(1分)又OMc平面BMD,PAg平面BMDPA//平面BMD(3分)PAc平面PAHG,平面PAHG∩平面BMD=GHPA//GH(5分)注:证明思路错误的不给分,证明过程缺少必要步骤的酌情扣分(2)方法一:由(1)可知:四边形PAHG是梯形且GH//-PA在△OMD中,GH/-OG是MD中点G到平面ABCD的距离为M到平面ABCD的距离的又M是PC的中点M到平面ABCD的距离为P到平面ABCD的距离的G到平面ABCD的距离为P到平面ABCD的距离的过P作PE⊥AD于点E平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PEc平面PADPE⊥平面ABCD√3G到平面ABCD的距离为-PE4×1×sin60(2)方法二:由(1)可知:四边形PAHG是梯形且GH/-PA长PG、AH相交于点FPGc面PCD,AHc面ACDF是面PCD与面ACD的公共点C而面PCD∩面ACD=CDF∈CD且DF=n4过P作PE⊥AD于点E平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PEc平面PADPE⊥平面ABCD又M是PC的中点,G是MD中点G到平面ABCD的距离为-PE(8分)VD-PAHG =VD-pF -VoG-DHF3836

解析】因为asin C-v3 ccos Bcos C3bcos2C,所以由正弦定理,得 sin Asin C=√3 sin Ccos bcos c √3 sin bcos2C,即 sin Asin c=√3cosC( sin Ccos B sin Bcos C),故 sin Asin C=√3 cos Csin A.又A∈(0,x),故sinA≠0所以sinC=3c0sC,即tnC=3,由C∈(0,),得C=3由余弦定理得c2=a2 62-2abos3=(a b)23ab=16,所以a b)2-16,故ab=3,故△ABC的面积S=1 absin C=133_332