2022语文衡水金卷答案

2022语文衡水金卷答案 ，目前答案易对网已经整理了2022语文衡水金卷答案 的各科答案和试卷，更多联考试卷请关注本网站。

8.解:(1)证明:在直角梯形ABCD中,因为点E,F分别是AB,CD的中点,所以EF∥BC,AE⊥EF.因为平面AEFD⊥平面EBCF,所以AE⊥平面EBCF,所以AE⊥EF,AE⊥BE,又BE⊥EF,所以可以建立如图所示空间坐标系Exyz翻折前,连接AC交EF于点G,此时点G使得AG GC最小EG=6BC=2又因为EA=EB=2则A(0,0,2),B(2,0,0),C(2,4,0),D(0,2,2),E(0,0.0,G(0、2,0),所以BD=(-2,2,2),C=(-2,-2,0)所以BD·C=(-2)×(-2) 2×(-2) 0=0,所以BD⊥CG.(2)设EG=k,因为AD∥平面EFCB,所以点D到平面EFCB的距离为即为点A到平面EFCB的距离因为S=[(3-b) 4×2=7-k,所以Vax=3·Saa形aC·AE、2(7-k)同理V=3Sx,BE=32 又因为2VsA=VDa,所以4(2 A)=2(7-k),所以k=1,即EG=1.设平面DBG的法向量为n1=(x,y,x)因为G(0,1,0),所以BG=(-2,1,0),BD=(-2,2,2),1·BD=0,2x 2y 2z=0即0取x=1,则y=2,z=-1,所以m1=(1,2,-1)平面BCG的一个法向量为n2=(0,0,1),平面BCG的一个法向量为n2=(0,0,1),则cos(m1,n2)因为所求二面角DBGC的平面角为锐角,所以此二面角的平面角的余弦值为

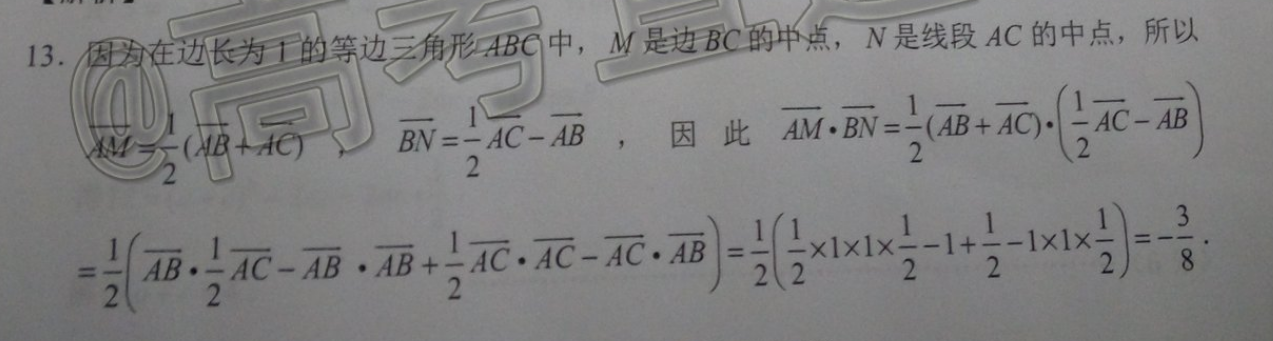
13.因发在边长为工的等边三角形ABC中,M是边BC的中点,N是线段AC的中点,所以B BN=-ACAB,因此AMBN1B AC).-AC-AB=AB·=AC-AB·AB =ACAC-AC·AB=5×1×1×--1 --1×12(22