2021高三全国100所名校文综

2021高三全国100所名校文综，目前我们已经整理了2021高三全国100所名校文综的各科答案和试卷，更多100所单元卷请关注本网站。

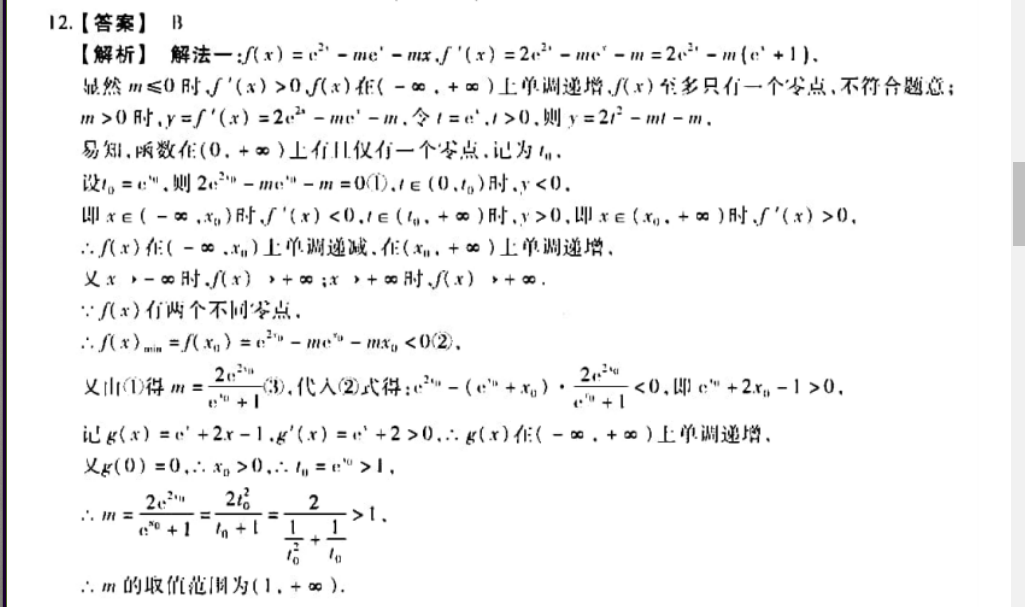
12.【答案】B【解析】解法一:f(x)=…-me'-mxJf'(x)=2e2-me'-m=2e'-m(e' 1)显然m≤0时√'(x)>0、f(x)在(-∞, ∞)上单调递增、f(x)至多只们一个点,不符合题意;m>0时,y=f'(x)=2c2-me'-m,令=e,>0,则y=212-m-m,易知,函数在(0, ∞)上有且仪有一个零点,记为ln,设t则2m=0①),∈(0,t0)时,y<0即x∈(-∞,x)时、'(x)<0,∈(l, ∞)时,y>0,即r∈(x ∞)时、f'(x)>0,∴∫(x)在(-∞,x)上单调递减,在(x, ∞)上单调递增又x-∞时、f(x), ∞;x ∞时、fx) ∞∵f(x)们两个不同苓点A(x)min=/(x,)m<02)又1得m÷2四”3.代入②式得:e-(c" n)·2<0,即c" 2r-1>0记g(x)=c' 2x-1,g'(x)=“' 2>0,g(x)在(-∞, ∞)上单调递增,又g(0)=00,∴ln2 1h m的取值范围为(1. ∞)解法二:当m=0时f(x)=2>0恒成立f(x)无兮点,不符介题意;当m≠0时,令f(x)=0得…-m'-mr=0∴(' x)m=“",∴iL g(r)(' t记h(x)=-…-2x 1,h'(x)=-…-2<0恒成立,∴h(x)在(-∞, ∞)上单调递减,又h(0)=0,∴r∈(-∞,0)时,h(x)>h(0)=0,;g'(x)>0,r∈(0, ∞)时,h(x)