2021届全国100所名校理数十二

2021届全国100所名校理数十二，目前我们已经整理了2021届全国100所名校理数十二的各科答案和试卷，更多100所单元卷请关注本网站。

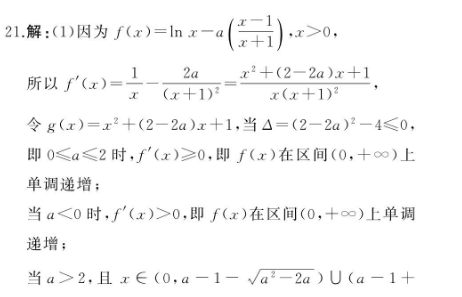
21.解:(1)因为f(x)=lnx-a(x-1x 1>0,所以f(x)=--x(x 12 (2-2a)x 112ax(x 1)2令g(x)=x2 (2-2a)x 1,当△=(2-2a)2-4≤0,即0≤a≤2时,f(x)≥0,即f(x)在区间(0, ∞)上单调递增;当a<0时,f(x)>0,即f(x)在区间(0, ∞)上单调递增;当a>2,且x∈(0,a-1-√a2-2a)U(a-1 √a2-2a, ∞)时,f(x)>0,即f(x)在区间(0,a1-√a2-2a),(a-1 √a2-2a, ∞)上单调递增;当x∈(a-1-√a2-2a,a-1 √a2-2a)时,f(x)<0,即f(x)在区间(a-1-√a2-2a,a-1 √a2-2a)上单调递减综上,当a≤2时,f(x)在区间(0, ∞)上单调递增;当a>2时,f(x)在区间(0,a-1-√a2-2a)和(a-1 √a2-2a, ∞)上单调递增,在区间(a-1-√a2-2a,a-1 √a2-2a)上单调递减.(6分)(2)因为单调函数至多有一个零点,所以a>2.因为f(1)=0,且a-1-√a2-2a<1 0,f(a-1 √a2-2a)<0.因为当x→0时,f(x)→∞;当x→ ∞时,f(x)→ ∞,而f(x)在区间(0,a-1-√a2-2a)和区间(a-1 √a2-2a, ∞)上单调递增,在区间(a-1-√a2-2a,a-1 √a2-2a)上单调递减,所以f(x)在区间(0,a-1-√a2-2a)上有且仅有一个零点,在区间(a-1-√a2-2a,a-1 √a2-2a)上有且仅有一个零点,在区间(a-1 √a2-2a,∞)上有且仅有一个零点,a-2a, ∞)时,f(x)>0,即f(x)在区间(0,a1-√a2-2a),(a-1 √a2-2a, ∞)上单调递增当x∈(a-1-√a2-2a,a-1 √a2-2a)时,f(x)<0,即f(x)在区间(a-1-√a2-2a,a-1 √a2-2a)上单调递减综上,当a≤2时,f(x)在区间(0, ∞)上单调递增;当a>2时,f(x)在区间(0,a-1-√a2-2a)和(a-1 √a2-2a, ∞)上单调递增,在区间(a-1-√a2-2a,a-1 √a2-2a)上单调递减.(6分)(2)因为单调函数至多有一个零点,所以a>2.因为f(1)=0,且a-1-√a2-2a<1 0,f(a-1 √a2-2a)<0.因为当x→0时,f(x)→∞;当x→ ∞时,f(x)→ ∞,而f(x)在区间(0,a-1-√a2-2a)和区间(a-1 √a2-2a, ∞)上单调递增,在区间(a-1√a2-2a,a-1 √a2-2a)上单调递减,所以f(x)在区间(0,a-1-√a2-2a)上有且仅有一个零点,在区间(a-1-√a2-2a,a-1 √a2-2a)上有且仅有一个零点,在区间(a-1 √a2-2a, ∞)上有且仅有一个零点,所以实数a的取值范围是(1, ∞)(12分)