2022-2023衡水金卷先享题 高三一轮复习40分钟周测卷(老高考)/理数(八)8答案

2022-2023衡水金卷先享题 高三一轮复习40分钟周测卷(老高考)/理数(八)8答案，目前答案易对网已经整理了2022-2023衡水金卷先享题 高三一轮复习40分钟周测卷(老高考)/理数(八)8答案的各科答案和试卷，更多联考试卷请关注本网站。

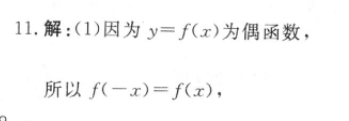
11.解：(1)因为y=f(x)为偶函数，所以f(一x)=f(x),即log(9-x 1)一kx=log(9 1) kx对于任意x∈R恒成立.于是2kx=log(9-2 1)-log(9 1)=log99 19-l0g(9 1)=-x恒成立，而x不恒为零，所以k=一是(8分)(2)由题意知方程1og,(g 1)-合x=名x十6无解，即方程1og(92 1)一x=b无解.令g(x)=log(9十1)一x,则函数y=g(x)的图象与直线y=b无交点，因为gx)=1og,g=1o8(1 ）,由1计>1,则gx)=log(1 g)>0,所以b的取值范围是（一∞，0].(14分)(3)由题意知方程3r十子=a·3”-专a有且只有一个实数根令3”=>0，则关于t的方程(a-1)2-Γ3at-1=0(记为(*)有且只有一个正根.若a=1,则1=一是，不合题意，舍去：若a≠1，则方程（￥）的两根异号或有两相等正根.由△=0，得a=子或-3：但a=→1=-2，不合题意，舍去：而a=-3→=号，符合题意。若方程()的两根异号。号<0=a>1,综上所述，实数a的取值范围是{一3}U(1, ∞).(20分)

20.己知椭圆C:x2 京=1(a>b>0)的高心率为5且短轴长等于双曲线：了-二=1的实轴长(1)求椭圆C的标准方程：(2)若A,B为椭圆C上关于原点O对称的两点，在圆D:x2 y=8上存在点P,使得△PAB为等边三角形，求直线AB的方程.【容]D号 y=2)=±5【解析】c5a 2【分析】(1)根据@意直接列方程b=1求解：a2=b2 c22)根据题意可得10=2y6设直线AB的方程代入求解，注意讨论斜率是杏存在.3【小问1详解】e=-=a依题意有b=1,解得a=2,c=√5.a2=b2 c2%圆C的标准方程为乏 2、【小问2详解】“成P在圆D: y=(22°上，∴lorl=2W2又：△PAB为等边三角形，且O为线段AB的中点，abm-p4o4-29①当直线AB的斜率不存在时，A,B为椭圆C的上下顶点，04小=126，不符合遥3②当直线AB的斜率存在时，设A(,y),直线AB的方程为y=kxy=,g以器24-原3哥-2955,直线AB的方程为：y=士55