2022年普通高等学校招生全国统一考试模拟演练数学1答案

2022年普通高等学校招生全国统一考试模拟演练数学1答案，目前我们已经整理了2022年普通高等学校招生全国统一考试模拟演练数学1答案的各科答案和试卷，更多试卷答案请关注本答案网。

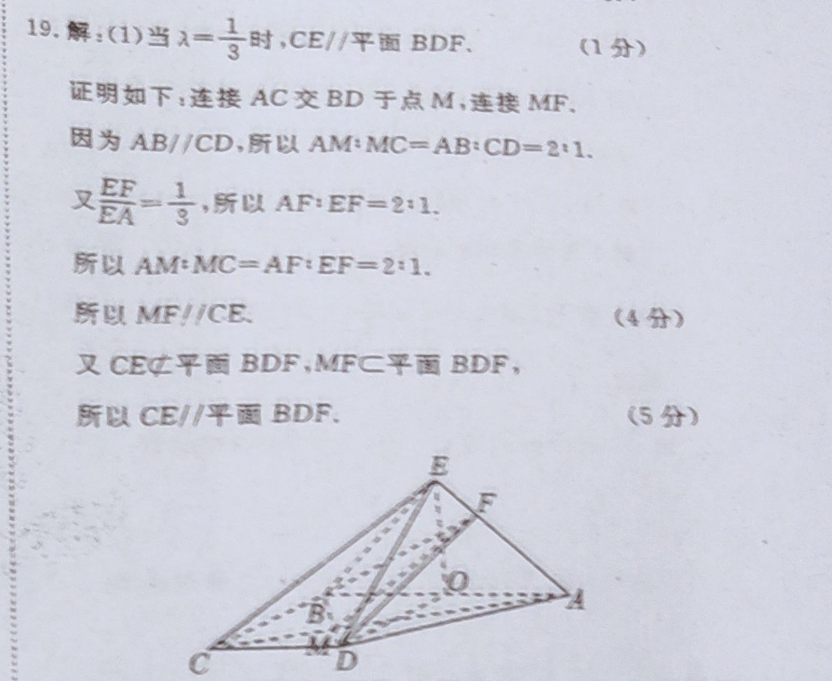
19.解:(1)当=时,CE/平面BDF(1分)证明如下:连接AC交BD于点M,连接MF因为ABCD,所以AMMC=ABCD=21又一3所以AFEF=2所以AMMC= AF:EF=2:1所以MF∥/CE(4分)又CE￠平面BDF,MFC平面BDF,所以CE∥/平面BDF(5分)BD(2)设点F到平面CDE的距离为d1,点A到平面CDE的距离为d2则由A=3得d=EE=1,即d1=-d2,(7分)AE 3取AB的中点O,连接EO,DO由EA=EB,得EO⊥AB,又平面EAB⊥平面ABCD,平面EAB门平面ABCDFAB所以OE⊥平面ABCD,所以OE⊥OD易得CD⊥平面EOD,所以CD⊥DE.由VE-ACD=VA-ce3°△D·EO=S△mEat得÷S(9分)CD BC·EO所以a2CD·DE1x÷ABOD2 OEZ12所以点F到平面CDE的距离为1-34-8(12分)

22.解:设P(P,0)为AB延长线上任意一点,则S△o S△op=S△p,即x3v3Xsin x√3 p xsin(0-2)=x3 p xsin02分化简得3=√3psin pcos0,3公即l的极坐标方程为p=T2sin(8 当P在AB之间或在BA的延长线上时,可得同样的方程5分(2)把=0代入P=cosb得OE|=1,由题知|OA=3,”36分把6=代入P=c0s0得ON|=;把θ=-代人p=得|OM8分2 sin(0 -)lOEI04OM3…NE∥AM10分