2022届超级全能生 5.1专享测试文科数学试题答案

2022届超级全能生 5.1专享测试文科数学试题答案，目前我们已经整理了2022届超级全能生 5.1专享测试文科数学试题答案的各科答案和试卷，更多试卷答案请关注本答案网。

21.【必备知识】本题考查的知识是“能利用基本初等函数的导数公式和导数的四则运算法则求简单函数的导数,并了解复合函数求导法则,能求简单复合函数的导数”,“了解函数的单调性与导数的关系;能利用导数研究函数的单调性,会求函数的单调区间(其中多项式函数不超过三次)”【关键能力】本题考查逻輯思维能力、运算求解能力【解题思路】(1)m=1f(x)=hnx-c-1求号/(x)=1 hnx-构造函数g(x)=f'(x)→g(x)≤0→f(x)的单调性→结果0 xlnxe>1,xlnx≤0f(x)<0将原问题转化为证构造函数xlnx→即证-Inx >0得证求导、构造函数p(x)=2e2(x-1)-x→p(x)的单调性p(1)=-1<0,pP(2)=0→h(x)在(1, ∞)上的单调性当x>1时,h(x)>0→f(x)<0解:(1)函数f(x)的定义域为(0, ∞)(1分)当m=一时,f(x)=xnx-e,则f'(x)=1 lnx-e(2分)记g(x)=1 lmx-e-1,则g(x)=1-e-1显然g'(x)在(0, ∞)上单调递减,且g'(1)=0(3分)所以当x∈(0,1)时,g'(x)>0,函数g(x)单调递增;当x∈(1, ∞)时,g'(x)<0,函数g(x)单调递减所以g(x)≤g(1)=1 ln1-1=0,即f'(x)≤0恒成立,(4分)所以函数f(x)在(0, ∞)上单调递减所以函数f(x)的单调递减区间为(0, ∞),无单调递增区间.(5分)(2)要证f(x)<0,只需证me>xlnx①当0 1,xnx≤0,m≥,不等式显然成立.(6分)②当x>1时,xnx>0,e'>e由m≥可得,me'≥-e于是原问题可转化为求证·e>xlnx,即证nx>0.(7分)令h(x)≈2e-2-1x,则h'(x)=2e2(x-1)-x(8分)令p(x)=2e2(x-1)-x,则p(x)=2xe"2-1,易知p'(x)在(0, ∞)上单调递增(9分)又p(1)=2-1<0,p(2)=30所以存在x∈(1,2)使得p'(x0)=010分)所以p(x)在(1,x)上单调递减,在(x, ∞)上单调递增,又p(1)=-1<0,p(2)=0,故当x∈(1,2)时,h(x)<0,h(x)单调递减当x∈(2, ∞)时,h(x)>0,h(x)单调递增,所以当x>1时,h(x)≥h(2)=1-ln2>0,即f(x)<0综上,f(x)<0.(12分)解题关键》求解本题第(2)问的关键有:(1)想到分0 1两种情况进行证明;(2)当x>1时,想到利用放缩法将愿问题转化为求证·e>xhx

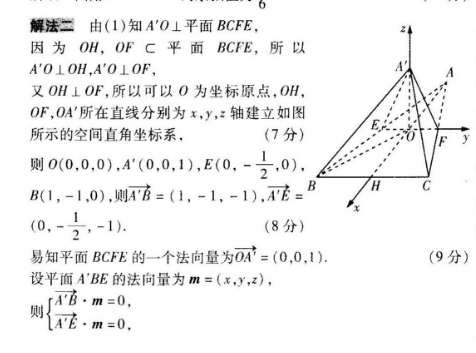
18.【试题情境】本題是基础性題目,属于课程学习情境,具体是数学推理学习情境【关键能力】本题考查空间想象能力、运算求解能力、逻辑恩维能力【学科素养】试题以平面图形的翻折为背景,要求考生分析几何元素间的位置关系、度量关系,体现的学科素养是数学探索【解题思路】(1)取BC的中点H,连接AH交EF于点O,连接A'O,BO,根据已知及翻折的性质得到A'O⊥EF,然后利用面面垂直的性质定理证得A'O⊥平面BCFE从而找到直线A'B与平面BCFE所成的角,最后利用解三角形的知识即可得解.(2)解法一先作辅助线,找到二面角A'-BE-C的平面角,然后利用解三角形的知识即可得解;解法二先棖据(1)建立空间直角坐标系,求出相关点的坐标,进而求出相关向量的坐标,然后求出相关平面的法向量,最后利用向量的夹角公式即可得解解:(1)如图,取BC的中点H,连接AH交EF于点O,则O为EF的中点,连接AO,BO.由题意知AH⊥BC,又平面AEF⊥平面BCFE,平面AEF∩平面::又EF∥BC,所以AO⊥EF,即AO⊥EF.(1分)BCFE=EF,AOC平面A'EF所以A'O⊥平面BCFE,(2分故∠A'BO即直线AB与平面BCFE所成的角,所以∠A'BO=则在Rt△A'BO中,4O=BO(3分)因为AB=AC=√5,BC=2,所以AH=2(4分)设AO=,则HO=2-,所以BO=√ (2-1=1,解得t=5所以4E=40=A0=5AB AH AH 8(6分)(2)解法一如图,过点O作OG⊥AB于点G连接A'G由(1)知A'O⊥平面BCFE,因为ABC平面BCFE,所以A'O⊥AB.(7分)又OG⊥AB,OG,AOC平面AOG,OG∩A'O=0,所以AB⊥平面A'OG,又A'GC平面A'OG,所以AB⊥A'G(8分)所以∠A'GO为二面角A-BE-C的平面角(9分)易知在Rt△A'CO中,AO=1,DF≈OA,DE1×,(10分)AL于是AG=0 0°√·}-√5(11分)所以cos∠A'CO=mAG 6所以二面角A'-BE-C的余弦值为(12分)解法二由(1)知A'O⊥平面BCFE,因为OH,OFC平面BCFE,所以A'O⊥OH,AO⊥OF,又OH⊥OF,所以可以O为坐标原点,OHOF,OA'所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,(7分)则0(0.0.0),A(0,0,1),E(0,-1,0),∠B(1,-1,0),则A言=(1,-1,-1),AEB(8分)易知平面BCFE的一个法向量为OA=(0,0,1)(9分)设平面A'BE的法向量为m=(x,y,z),B·m=0AE0取y=2,则m=(l(11分)所以cos(O,m)=o41·m1×√ 4 1由图知二面角A-BE-C为锐二面角,所以二面角A'-BE-C的余弦值为√6(12分)6图解题关键》解决翻折问题的关键是确定翻折前后各量之间的关系,准确把握翻折前后的两个“不变关系”:①与折痕垂直的线段,翻折前后垂直关系不变;②与折痕平行的线段,翻折前后平行关系不变