2021-2022学年度高三年级第三次模拟4月联考文科数学答案

2021-2022学年度高三年级第三次模拟4月联考文科数学答案，目前答案易对网已经整理了2021-2022学年度高三年级第三次模拟4月联考文科数学答案的各科答案和试卷，更多联考试卷请关注本网站。

8.向预测……抛物线是历年高考常考内容,主要考查三个方面:一是其定义与标准方程;二是几何性质;三是直线与抛物线的位置关系.其中定义及其应用是考查重点的思路……设AF|=m,|BF=n,过点A,B分别作抛物线C的准线的垂线,垂足分别为A1,B1,由抛物线的定义可得|AA1=m,IBB1|=n,因为D为线段AB的中点,所以|DEAAI IBB,I m n由FA FB=AB1,易得AF⊥BF,所以AB1=m2 n2,所以DE (m n) n2 2nAB|24(m2 n2)4(1 m2甲)≤4(1 2m)=,当且仅当时取等号,所以AB的最大值为y2,故选C考答案……C命题人讲评·【命制过程】试题以抛物线为背景,主要考查抛物线的几何性质【临考提醒】抛物线性质的应用技巧(1)利用抛物线方程确定及应用其焦点、准线时,关键是将抛物线方程化成标准方程(2)要结合图形分析,灵活运用平面图形的性质简化运算(3)本题利用换元法、基本不等式求得所求参数的取值范围

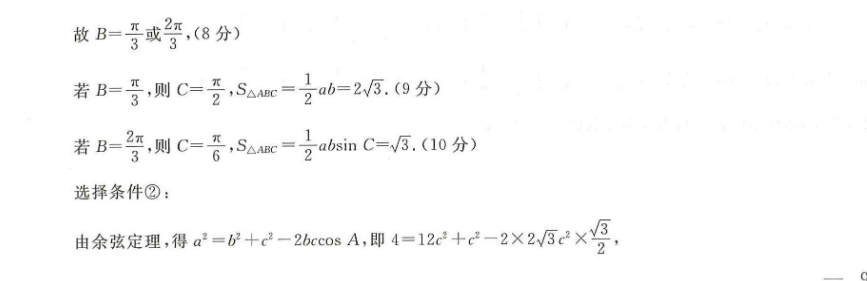
17.向预测……解三角形是高考的常考内容,属中档题.高考对本部分的考查主要有三个方面:(1)正、余弦定理与三角恒等变换的综合应用:解三角形、边角统一思想与三角恒等变换的综合应用求角的三角函数值或者范围;(2)利用正余弦定理解决图形问题:分析给出的图形,将已知条件先集中到某个三角形中,解三角形,再依次解其他三角形,直至求出结果;(3)正、余弦定理的实际应用:建立三角模型,利用解三角形求出边或角●思路……先将已知条件“ bsin b csin c=(23bsnC a)snA”利用正弦定理、余弦定理转化、化简,然后再结合条件“a=2”和选择的某个条件求解三角形的面积注意要从三个待选条件只选一个计算参考答案…因为 brinG csiC=(23 bsin c a)sinA,所以由正弦定理可得b2 c2=(23 bsin c a)a,即b2 c2-a2=23 absin C,所以由余弦定理可得2 bcos a=2√3 absin C,所以 sin ccos a=√3 sin asin o,(3分)因为sinC≠0,所以cosA=3sinA,因为A∈(0,x),所以A=·(5分)选择条件①由正弦定理,得sinA=sinB即23sin t sin B'解得sinB=y3故B=2或,(8分)若B=3,则C=2,S△m=2b=2.(9分)若B=2x,则C=x,S△ABC= -absin C=3.(10分)选择条件②:由余弦定理,得a=b c-20c0A,甲4=12 -2×25xg,整理得4=72,解得c=22,(8分)所以△ABC的面积为S=1ksmA=1×23c×1=27(10分)选择条件③由余弦定理,得a2=(b c)2-2bc-2 bcos A即4=4-2k-2c,3,解得bc=12(2-3),(8分)所以△ABC的面积为S=2如mA=2x(24-12)xsm=6-3.(0分)命题人讲评【命制过程】考查正、余弦定理以及三角形面积公式的应用.设置开放性条件,给考生创造入口宽的解题背景,借以考查考生自主选择条件熟练运用所学知识分析问题、解决问题的能力方法技巧】1,对于面积公式S=2bnC=2 -actin B=2 bcsin a,一般是已知哪一个角就使用哪一个公式2.与面积有关的问题,一般要用到正弦定理或余弦定理进行边和角的转化