2022届金太阳广东省3月联考(804·GD)数学试题答案

2022届金太阳广东省3月联考(804·GD)数学试题答案，目前答案易对网已经整理了2022届金太阳广东省3月联考(804·GD)数学试题答案的各科答案和试卷，更多联考试卷请关注本网站。

16.-2分，第二空3分)【解析】设∠BAC=A.以A为原点，AC所在直线为2角坐标系（图略），则A(0,0),C(1,0).设B(4cos0,4sin0).所以AB=(4cos0,4sin0),AC=(1,0).所以2AB 2AC=(2 2c0s0,2sin01=√8 8cos0=25.所以c0s0=7.因为0<0<，所以0=号.所以B(2,2W5).设P(m,5m)(0≤m≤2)，则P市.Pt=(2-m,25-m）1-m,-5m)=4m-9m 2=4(m-号）-8所以当m=号时，P咕·P心取得最小值一磐16

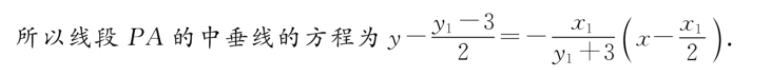
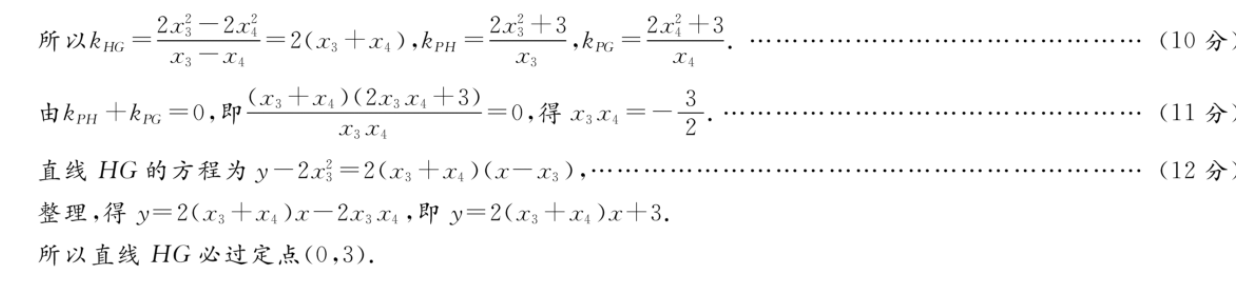
20.(本小题满分12分)【解析】设A(x1,y1),B(x2,y2).(1)设直线AB的方程为y=kx一1.联立方程，得y=4x2-3,化简，得x2一4kx一8=0.y=kx一1，所以△=16k2十32>0，x1十x2=4k,x1x2=一8.………………………(2分)若直线L与点M的轨迹有交点，则PA⊥PB.易知P(0,-3),由P才·PB=0,得x1x2十yy2十3(y十2)十9=0.因为y1十y=4k2一2，y1y2=一12k2十1，代入上式不成立，所以直线l与点M的轨迹没有交点.…………（4分)(2)因为点M是△PAB的外接圆的圆心，所以，点M是△PAB三条边的中垂线的交点.设线段PA的中点为F,线段PB的中点为E.因为P(0,一3)，所以F(号，当，3），E(受，，3），A=当 3，B=当 3……………………………………（5分）所以线段PA的中垂线的方程为y一2=一3(x一受）2因为A在抛物线C上，所以y十3=示.所以PA的中垂线的方程为)一琴 3=一(：一号)），即y=一手十君-1.同理可得线段PB的中垂线的方程为y=一4x十-1.48(6分)y=-4 x近一1，xM=-1(x十x2)32联立方程，得解得(7分)y=一4x吃81,w=好 十西x2-88由(1)可得x1十x2=4k,x1x2=一8.所以w=-二8X4=k,w= 店十 2=（西 )》=2，即Mk,2).32881所以x,=之yM.所以点M的轨迹方程为x2=2山.………………………………………(9分)方法一：设直线GH的方程为y=mx十b,且m≠0，b>0,G(x3,y3),H(x4,y).x2=联立方程，得2y,化简，得2-子mrb=0.、y=mx十b所以4=}m 26>0,x十五=7m,4=-b...............(10分)根据题意，得直线PG与直线PH的斜率之和为0.所以kG十kpH=当 3 y十3=4y十34十3(x十x)X3 XA=4(m3 b) (mx b)） 3(十x》=0.……(11分)X3X4所以x,(m十b) x(m b) 3(x十)=2mx (6 3)(x十x)=2m(-合) (b 3)·罗=罗63)=0..m≠0，∴.b=3.所以直线GH必过定点(0,3).………………（12分)方法二：设H(x3,2x号)，G(x4,2x)是满足条件的两点，则x3十x4≠0.所以kc2g-2=2(3十x),kpm=2x号 2x 3,kG=(10分x3一x4C3X4由pm十=0，即十2十3》=0，得x,=X3XA2.(11分直线HG的方程为y一2x=2(x3十x4)(x一x3）,……(12分整理，得y=2(x3十x4)x一2x3x4,即y=2(x3十x4)x十3.所以直线HG必过定点(0,3).