2022普通高校招生全国统一考试·模拟信息卷QG(二)2文科数学答案

2022普通高校招生全国统一考试·模拟信息卷QG(二)2文科数学答案，目前我们趣对答案已经整理了2022普通高校招生全国统一考试·模拟信息卷QG(二)2文科数学答案的各科答案和试卷，更多试卷答案请关注本趣对答案。

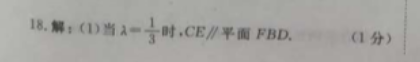
18.解:(1)当A=于时,CE∥平面FBD(1分)证明如下:连接AC,交BD于点M,连接MF因为AB∥CD所以AMMC=ABCD=211又E一}E所以FAEF=211所以AMMC=AFEF=21所以MF∥CE(4分)又MFC平面BDF,CE平面BDF,所以CE∥平面BDF(5分)(2)取AB的中点O则EO⊥AB.又因为平面ABE⊥平面ABCD,平面ABE∩平面ABCD-AB所以EO⊥平面ABCD因为ODC平面ABCD,所以EO⊥ODBC⊥CD,及AB=2CD得OD⊥AB,由OB,OD,OE两两垂直,建立如图所示的空间直角坐标系Oxye因为△EAB为等腰直角三角形,AB=2BC=2CD,所以OA=OB=OD=OE设OB=1,所以000100ABOD(0,1,0),E(0,0,1)所以A一(200=C0(7分)3所以=(号…-号)设平面BDF的法向量为n=(x,y,x)则有FB所以x-30取x=1,得n=(1,1,2)(9分)设直线AB与平面BDF所成的角为B,则如 8-lcoscAH,m)1=A方mABlIn2×1 0×1 02√ 1 222即直线AB与平面BDF所成角的正弦值为

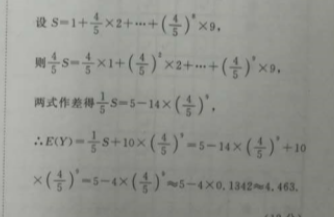
21.解:(1)由题意知:中间值2610概率0.10.150.450.20.1所以样本平均数为x=2×0.1 4×0.15 6×0.458×0,2 10×0.1=6.1(万元),所以Z~N(6.1,2.12),所以(-20g a)=(1.9,8.2),P(p=2<2< a)=方P(p=